The Bias Tape Formula Conundrum
- Published:
- Length: 1091 words
- Reading Time: 6 minutes
There is an accepted, "standard" formula for making your own continuous bias tape. However, trying to figure it out on your own is hard. There's quite a bit of misinformation floating about the internet that complicates the situation. Furthermore, the formula itself can't always be correct (this post is going to explain why).
(If you're not sure how to make your own continuous bias tape, stop right here! Go to this post that explains the process. Then, come back here and read about the technical details.)
Buckle up, everyone. It's time for some MATH!
What's the formula?
The standard formula for calculating the size of fabric square needed to create any given amount of continuous bias tape looks like this:

It looks scary, but the verbal translation is "the fabric square size is equal to the square root of the area of your bias tape, plus 1/2" for seam allowance." Let's test it:
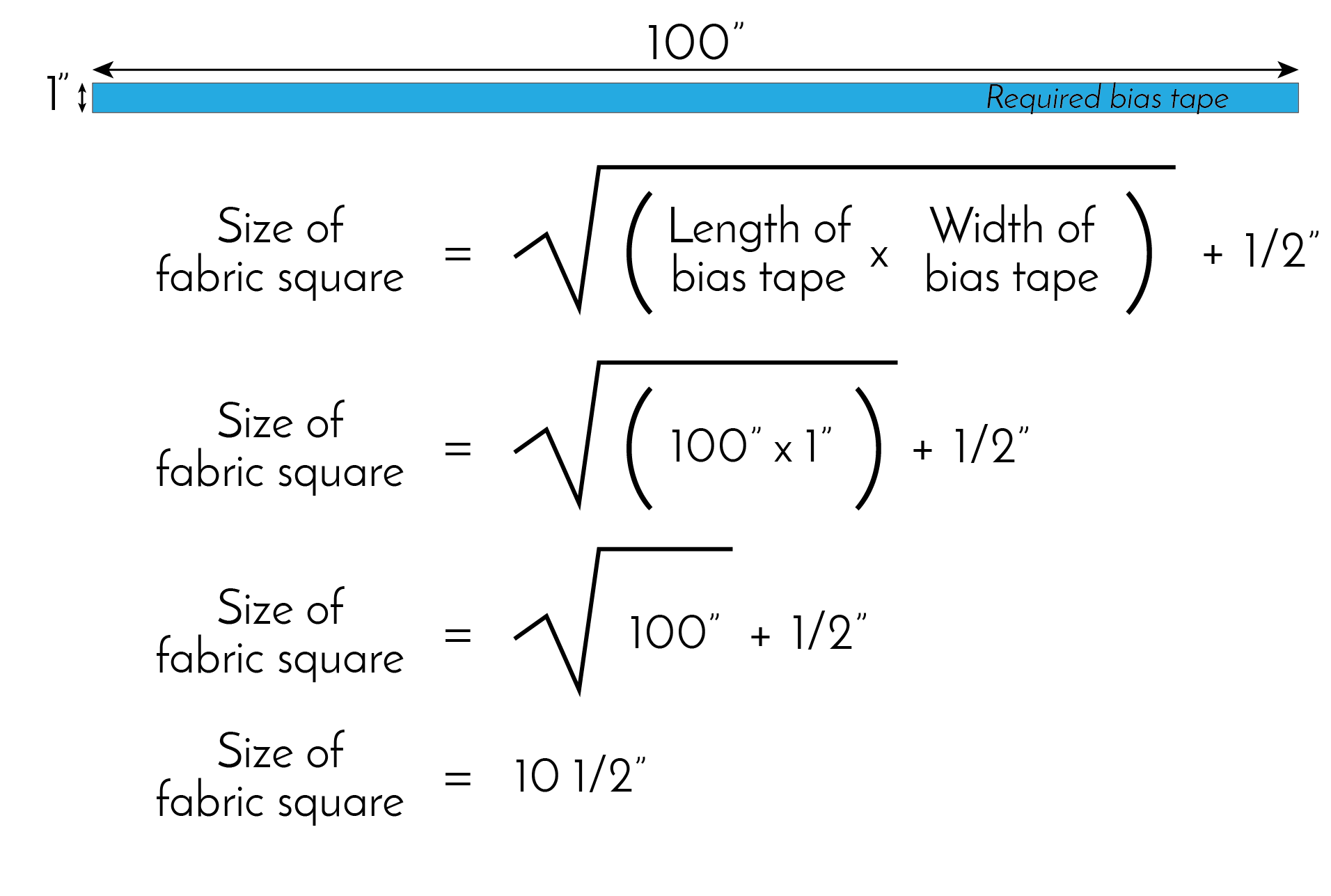
In other words, the standard formula tells us that we need a 10 1/2" square of fabric to make 100" of 1" wide bias tape. Seems straight-forward. But does it work?
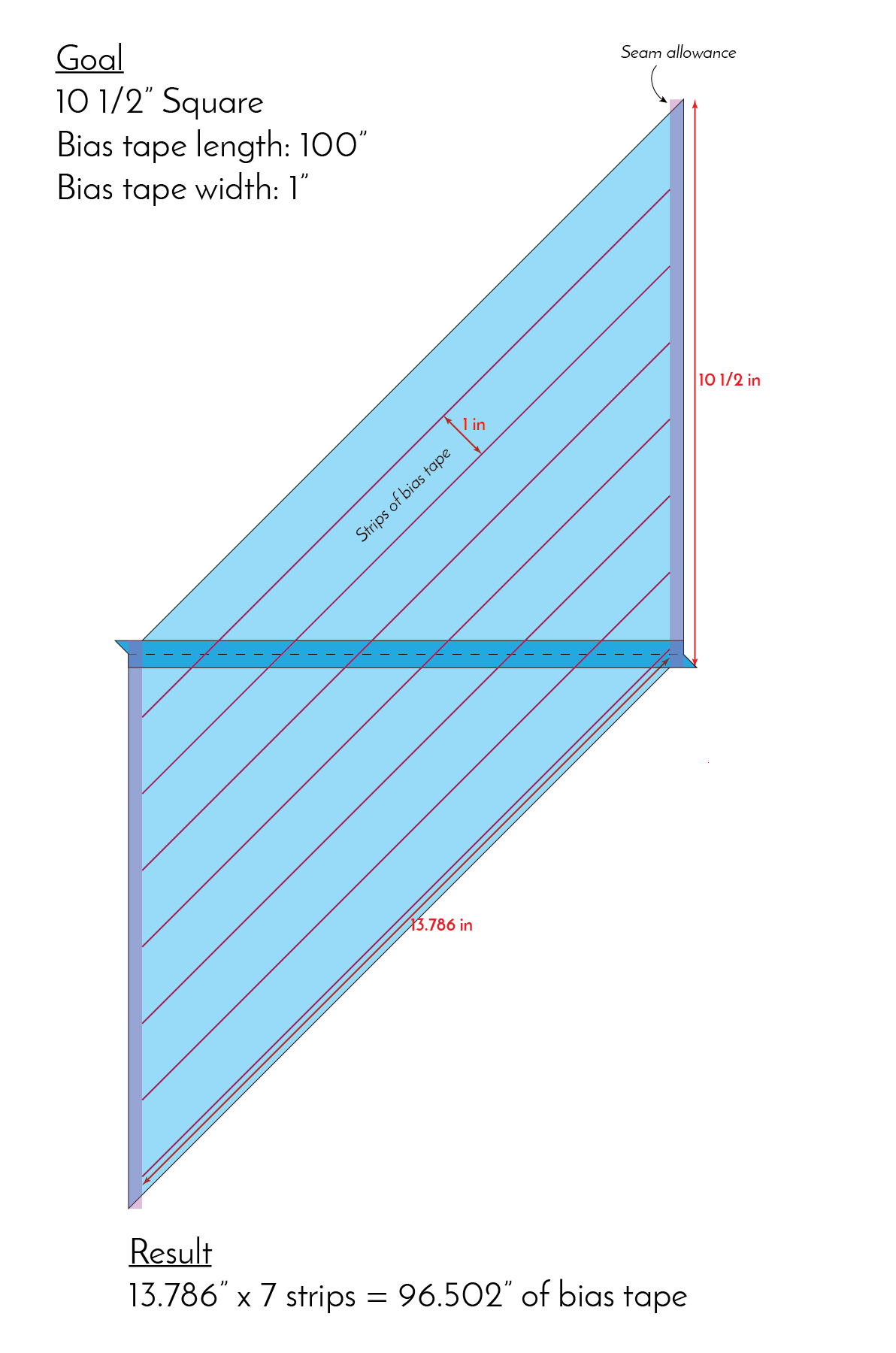
The above image represents the square of fabric after the first seam is sewn and pressed open. The purple diagonal lines represent the guide lines one would draw on the fabric before sewing the second seam (later on, these lines will get cut with scissors to create the bias tape). The semi-transparent rectangles on either side of the parallelogram represent seam allowance for the 2nd seam.
Since we are making 1" wide bias tape, the purple lines are 1" apart. I've taken the length of the drawn line (excluding seam allowance) and multiplied it by 7 (because there are 7 1" wide strips). The result is less than satisfactory: 96 1/2".
It appears that our 10 1/2" square does not, in fact, yield 100" of bias tape. We are a full 3 1/2" short. It's a perfect example of why the standard formula is unreliable. Let's break it down.
Why the standard formula doesn't always work
On the surface, the standard formula seems like it should work. It gives us a square that has the same area as the bias tape we need, which means they both have the same amount of fabric. The problem is that the formula calculates the linear size of a square, but bias tape is cut...on the bias. (In math terms, bias tape is cut on the hypotenuse, or 45 degree diagonal.)
Let's take another look at the above example. This time I've added some additional measurements.
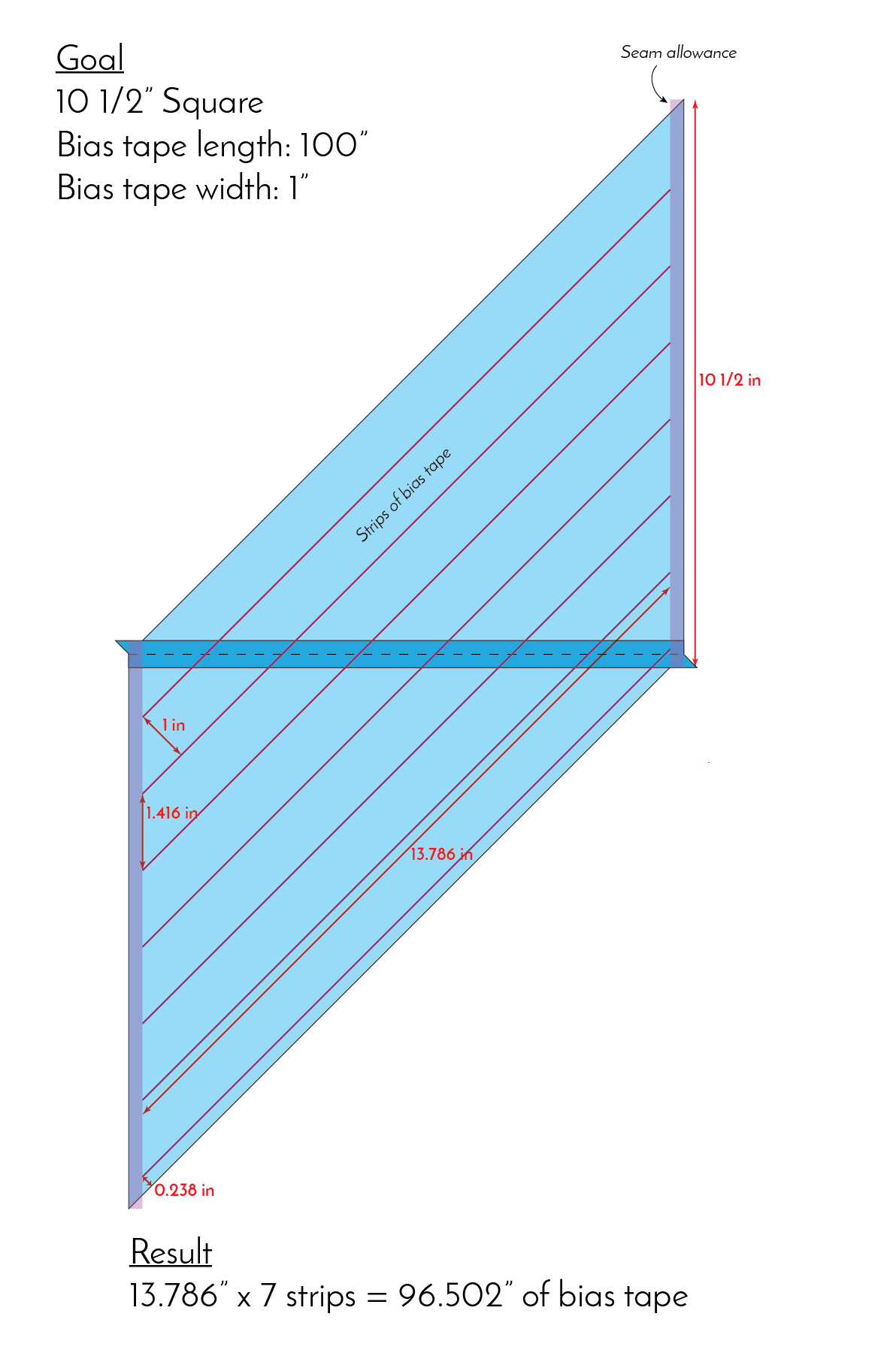
The drawn lines are parallel to the diagonal (long) sides of the parallelogram, spaced 1" apart. However, where those lines intersect the linear (short) sides, they are 1.416" apart. The height of our square, 10 1/2", is not evenly divisible by 1.416". This means we end up with wasted fabric (see the almost 1/4" strip at the bottom of the diagram.)
The result from the formula (excluding the extra 1/2" for seam allowance) used exactly the same amount of fabric as needed for the bias tape. There was no margin of error.
What about rounding?
Some websites advocating the standard formula direct users to round up to the nearest inch. Not every length of bias tape creates a nice, even size number for the fabric square, so it makes sense to round. Rounding will also cause the formula to be accurate more often (since rounding up adds more fabric), but it's still not accurate 100% of the time.
Let's look at a new example. Say I need to make 100" of 2" bias tape. According to the formula, and then rounding up to the nearest inch, I need a 15 1/2" square (including seam allowance). Take a look:

Let's see if it works:
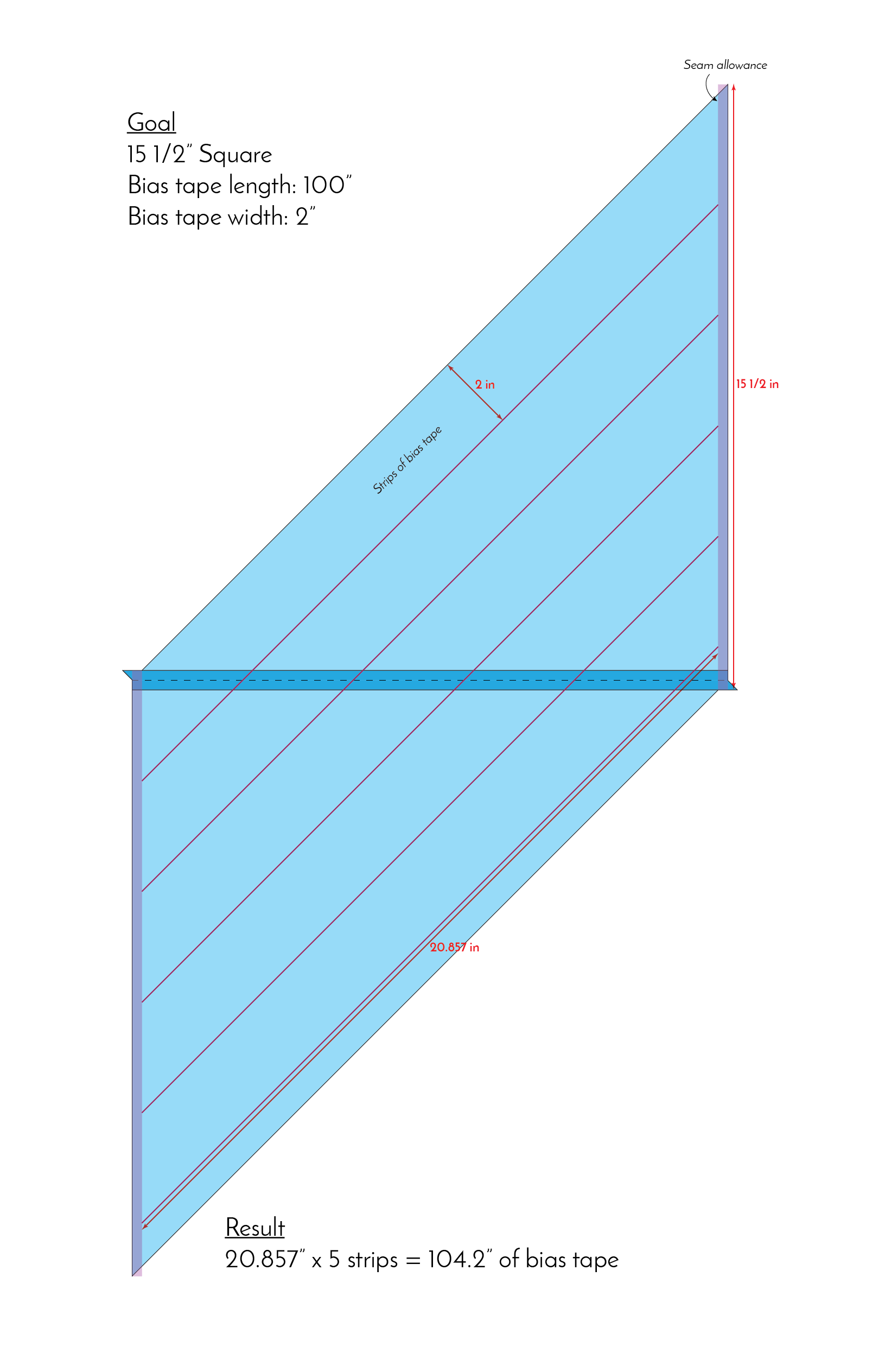
As you can see above, the 15 1/2" resulted in 104" of bias tape, which is actually 4" more than we needed. The rounding obviously worked. Problem solved, right? Not so fast.
We now know that the maximum 2" bias tape that can be produced from a 15 1/2" square is 104". Let's try another calculation. This time, I need 110" of 2" bias tape:

Because of rounding, the standard formula tells me I still need a 15 1/2" square, which simply isn't correct.
Rounding up 2" is an option, but the problem there is wasted fabric, either in the form of unneeded bias tape or a strip that gets cut off and discarded before sewing the second seam. You could also try adding lots of extra bias length, with the hope that you end up with the amount you actually need. Neither of those solutions is ideal.
The truth is, there's no real way to know if the square size calculated using the standard formula is ever correct.
What other option do we have?
I took this problem to my husband, who is a software developer. He wrote a calculator for me that takes into account the hypotenuse dimension of the bias tape when calculating square size, which has resulted in amazingly accurate and efficient results. His calculator figures out the most efficient square size to produce the desired length of bias tape while wasting the least amount of fabric. It's wonderful, and I've used it to calculate the bias tape for the every quilt I've made since he wrote it.
Although his calculator works very well, it's currently only a command line application. This means there's no interface to look at and no way to use it unless you know how to write code.
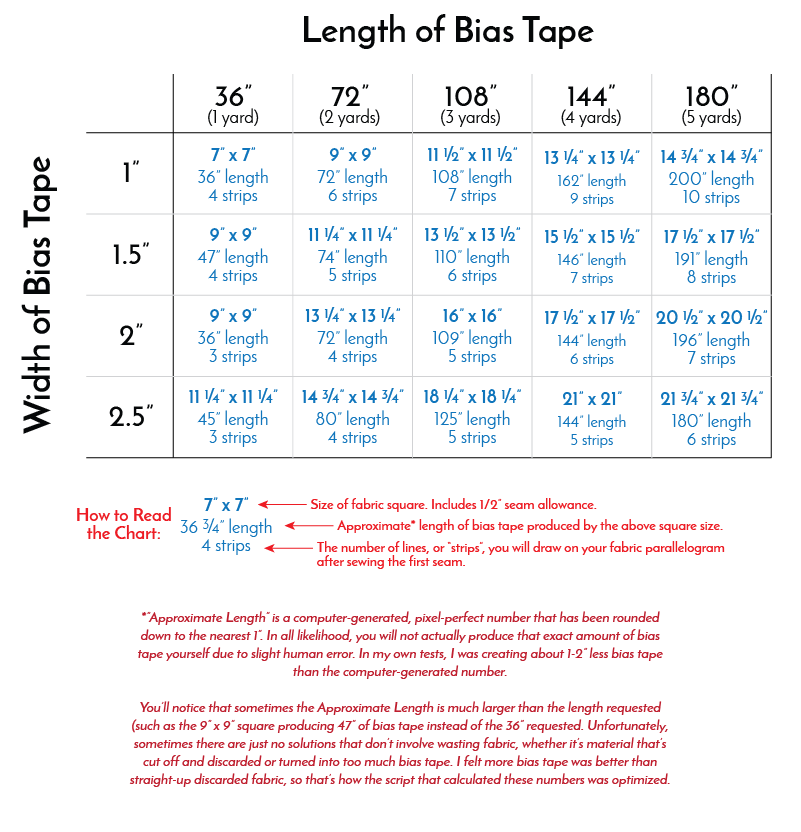
Someday I'd like to offer Alex's calculator as a web app with user interface free-to-use on this website. However, that takes a lot of time, since Alex will need to rewrite the entire thing. Until then, the best I can offer is a chart with various bias tape widths and lengths that was produced using his calculator.